👩‍💻 Lab 1

Fine-grained & Channel Pruning

Lab 1 Pruning

이번 Lab 1 Pruning은 다음과 같은 목표와 내용으로 구성되어 있습니다. 아래 버튼을 눌러 Colaboratory에서 바로 실행할 수 있습니다.

Goals

• pruning의 기본 개념을 이해합니다.
• fine-grained pruning을 구현하고 적용합니다.
• channel pruning을 구현하고 적용합니다.
• pruning으로부터의 성능 개선(예: 속도 향상)에 대한 기본적인 이해를 얻습니다.
• 이러한 pruning 접근 방식 간의 차이점과 tradeoffs를 이해합니다.

Contents

이 실습에는 Fine-grained Pruning과 Channel Pruning의 두 가지 주요 섹션이 있습니다.

총 9개의 질문이 있습니다:

• Fine-grained Pruning에 대해서는 5개의 질문이 있습니다 (Question 1-5).
• Channel Pruning에 대해서는 3개의 질문이 있습니다 (Question 6-8).
• Question 9는 fine-grained pruning과 channel pruning을 비교합니다.

실습노트에 대한 설정 부분(Setup)은 Colaboratory Note를 열면 확인하실 수 있습니다. 포스팅에서는 보다 실습내용에 집중할 수 있도록 생략되어 있습니다.

weight 값의 분포를 살펴봅시다.

pruning으로 넘어가기 전에, dense 모델에서 가중치 값의 분포를 살펴봅시다.

def plot_weight_distribution(model, bins=256, count_nonzero_only=False):
    fig, axes = plt.subplots(3,3, figsize=(10, 6))
    axes = axes.ravel()
    plot_index = 0
    for name, param in model.named_parameters():
        if param.dim() > 1:
            ax = axes[plot_index]
            if count_nonzero_only:
                param_cpu = param.detach().view(-1).cpu()
                param_cpu = param_cpu[param_cpu != 0].view(-1)
                ax.hist(param_cpu, bins=bins, density=True,
                        color = 'blue', alpha = 0.5)
            else:
                ax.hist(param.detach().view(-1).cpu(), bins=bins, density=True,
                        color = 'blue', alpha = 0.5)
            ax.set_xlabel(name)
            ax.set_ylabel('density')
            plot_index += 1
    fig.suptitle('Histogram of Weights')
    fig.tight_layout()
    fig.subplots_adjust(top=0.925)
    plt.show()

plot_weight_distribution(model)

Question 1 (10 pts)

위 weight 히스토그램들을 보고 다음 질문에 답해 주세요.

Question 1.1 (5 pts)

각기 다른 계층에서 weight 분포들의 공통적인 특성은 무엇인가요?

Your Answer:

mean이 0인 normal 분포를 따르고 있다 (backbone의 경우, classifier 제외)

Question 1.2 (5 pts)

이러한 특성들이 pruning에 어떻게 도움이 되나요?

Your Answer:

0이 많으므로, 계산하지 않거나 없앨 수 있다.

Fine-grained Pruning

이 섹션에서는 fine-grained pruning을 구현하고 수행할 것입니다.

Fine-grained pruning은 가장 중요도가 낮은 synapses를 제거합니다. Fine-grained pruning 후에는 가중치 텐서 \(W\)가 sparse해지며, 이는 sparsity로 설명할 수 있습니다:

\(\mathrm{sparsity} := \#\mathrm{Zeros} / \#W = 1 - \#\mathrm{Nonzeros} / \#W\)

여기서 \(\#W\)는 \(W\)의 element 수입니다.

실제로, 목표 sparsity \(s\)가 주어지면, 가중치 텐서 \(W\)는 제거된 가중치를 무시하기 위해 이진 마스크 \(M\)과 곱해집니다:

\(v_{\mathrm{thr}} = \texttt{kthvalue}(Importance, \#W \cdot s)\)

\(M = Importance > v_{\mathrm{thr}}\)

\(W = W \cdot M\)

여기서 \(Importance\)는 \(W\)와 동일한 형태의 중요도 텐서이며, \(\texttt{kthvalue}(X, k)\)는 텐서 \(X\)의 \(k\)번째로 작은 값을 찾으며, \(v_{\mathrm{thr}}\)는 임계값입니다.

Magnitude-based Pruning

Fine-grained pruning에 있어서 널리 사용되는 importance(중요도)는 weight 값의 크기, 즉,

\(Importance=|W|\)

입니다. Magnitude-based Pruning으로 알려져 있습니다 (Learning both Weights and Connections for Efficient Neural Networks 참조).

Question 2 (15 pts)

다음 magnitude-based fine-grained pruning 함수를 완성해 주세요.

Hint:

• 1단계에서는 pruning 후에 0의 개수(num_zeros)를 계산합니다. num_zeros는 정수여야 합니다. 부동 소수점 숫자를 정수로 변환하기 위해 round() 또는 int()를 사용할 수 있습니다. 여기서는 round()를 사용합니다.
• 2단계에서는 가중치 텐서의 importance를 계산합니다. Pytorch는 torch.abs(), torch.Tensor.abs(), torch.Tensor.abs_() API를 제공합니다.
• 3단계에서는 threshold를 계산하여 threshold보다 중요도가 낮은 모든 synapses가 제거되도록 합니다. Pytorch는 torch.kthvalue(), torch.Tensor.kthvalue(), torch.topk() API를 제공합니다.
• 4단계에서는 threshold를 기반으로 pruning mask를 계산합니다. mask에서 1은 synapse가 유지됨을 나타내고, 0은 synapse가 제거됨을 나타냅니다. mask = importance > threshold. Pytorch는 torch.gt() API를 제공합니다.

def fine_grained_prune(tensor: torch.Tensor, sparsity : float) -> torch.Tensor:
    """
    magnitude-based pruning for single tensor
    :param tensor: torch.(cuda.)Tensor, weight of conv/fc layer
    :param sparsity: float, pruning sparsity
        sparsity = #zeros / #elements = 1 - #nonzeros / #elements
    :return:
        torch.(cuda.)Tensor, mask for zeros
    """
    sparsity = min(max(0.0, sparsity), 1.0)
    if sparsity == 1.0:
        tensor.zero_()
        return torch.zeros_like(tensor)
    elif sparsity == 0.0:
        return torch.ones_like(tensor)

    num_elements = tensor.numel()

    ##################### YOUR CODE STARTS HERE #####################
    # Step 1: calculate the #zeros (please use round())
    num_zeros = round(num_elements * sparsity)
    # Step 2: calculate the importance of weight
    importance = torch.abs(tensor)
    # Step 3: calculate the pruning threshold
    threshold = torch.kthvalue(torch.flatten(importance), num_zeros)[0]
    # Step 4: get binary mask (1 for nonzeros, 0 for zeros)
    mask = importance > threshold

    ##################### YOUR CODE ENDS HERE #######################

    # Step 5: apply mask to prune the tensor
    tensor.mul_(mask)

    return mask

위에서 정의한 fine-grained pruning 기능을 확인하기 위해, 더미 텐서에 위 함수를 적용해 봅시다.

test_fine_grained_prune()

* Test fine_grained_prune()
    target sparsity: 0.75
        sparsity before pruning: 0.04
        sparsity after pruning: 0.76
        sparsity of pruning mask: 0.76
* Test passed.

Question 3 (5 pts)

마지막 셀은 pruning 전후의 텐서를 그립니다. 0이 아닌 값은 파란색으로, 0은 회색으로 표시됩니다. 다음 코드 셀에서 target_sparsity의 값을 수정하여 pruning 후 sparse 텐서에 0이 아닌 값이 10개만 남도록 해 주세요.

##################### YOUR CODE STARTS HERE #####################
# sparsity:=#Zeros/#𝑊=1−#Nonzeros/#𝑊
# 1 - 10/25
target_sparsity = 0.6 # please modify the value of target_sparsit
##################### YOUR CODE ENDS HERE #####################
test_fine_grained_prune(target_sparsity=target_sparsity, target_nonzeros=10)

* Test fine_grained_prune()
    target sparsity: 0.60
        sparsity before pruning: 0.04
        sparsity after pruning: 0.60
        sparsity of pruning mask: 0.60
* Test passed.

이제 fine-grained pruning 함수를 전체 모델을 pruning하는 클래스로 래핑합니다. FineGrainedPruner 클래스에서는 모델 가중치가 변경될 때마다 마스크를 적용하여 모델이 항상 sparse 상태를 유지할 수 있도록 pruning 마스크 기록을 가지고 있어야 합니다.

class FineGrainedPruner:
    def __init__(self, model, sparsity_dict):
        self.masks = FineGrainedPruner.prune(model, sparsity_dict)

    @torch.no_grad()
    def apply(self, model):
        for name, param in model.named_parameters():
            if name in self.masks:
                param *= self.masks[name]

    @staticmethod
    @torch.no_grad()
    def prune(model, sparsity_dict):
        masks = dict()
        for name, param in model.named_parameters():
            if param.dim() > 1: # we only prune conv and fc weights
                masks[name] = fine_grained_prune(param, sparsity_dict[name])
        return masks

Sensitivity Scan

각 레이어는 모델 성능에 대해 각각 다르게 기여합니다. 각 레이어에 적절한 sparsity를 결정하는 것은 어려운 일입니다. 널리 사용되는 접근 방식은 sensitivity scan입니다.

sensitivity scan 동안, 각 시간마다 하나의 레이어만을 prune하여 accuracy 저하를 관찰합니다. 다양한 sparsities를 스캔함으로써, 해당 레이어의 sensitivity curve (즉, 정확도 대비 sparsity)를 그릴 수 있습니다.

다음은 sensitivity curves의 예시 그림입니다. x축은 sparsity 또는 #parameters가 감소한 비율 (즉, sparsity)입니다. y축은 검증 정확도입니다. (Learning both Weights and Connections for Efficient Neural Networks의 Figure 6)

다음 코드 셀은 스캔된 sparsities와 각 가중치가 prune될 때의 정확도 리스트를 반환하는 sensitivity scan 함수를 정의합니다.

@torch.no_grad()
def sensitivity_scan(model, dataloader, scan_step=0.1, scan_start=0.4, scan_end=1.0, verbose=True):
    sparsities = np.arange(start=scan_start, stop=scan_end, step=scan_step)
    accuracies = []
    named_conv_weights = [(name, param) for (name, param) \
                          in model.named_parameters() if param.dim() > 1]
    for i_layer, (name, param) in enumerate(named_conv_weights):
        param_clone = param.detach().clone()
        accuracy = []
        for sparsity in tqdm(sparsities, desc=f'scanning {i_layer}/{len(named_conv_weights)} weight - {name}'):
            fine_grained_prune(param.detach(), sparsity=sparsity)
            acc = evaluate(model, dataloader, verbose=False)
            if verbose:
                print(f'\r    sparsity={sparsity:.2f}: accuracy={acc:.2f}%', end='')
            # restore
            param.copy_(param_clone)
            accuracy.append(acc)
        if verbose:
            print(f'\r    sparsity=[{",".join(["{:.2f}".format(x) for x in sparsities])}]: accuracy=[{", ".join(["{:.2f}%".format(x) for x in accuracy])}]', end='')
        accuracies.append(accuracy)
    return sparsities, accuracies

다음 셀들을 실행하여 sensitivity curves를 그려주세요. 완료하는 데 약 2분 정도 걸릴 것입니다.

sparsities, accuracies = sensitivity_scan(
    model, dataloader['test'], scan_step=0.1, scan_start=0.4, scan_end=1.0)

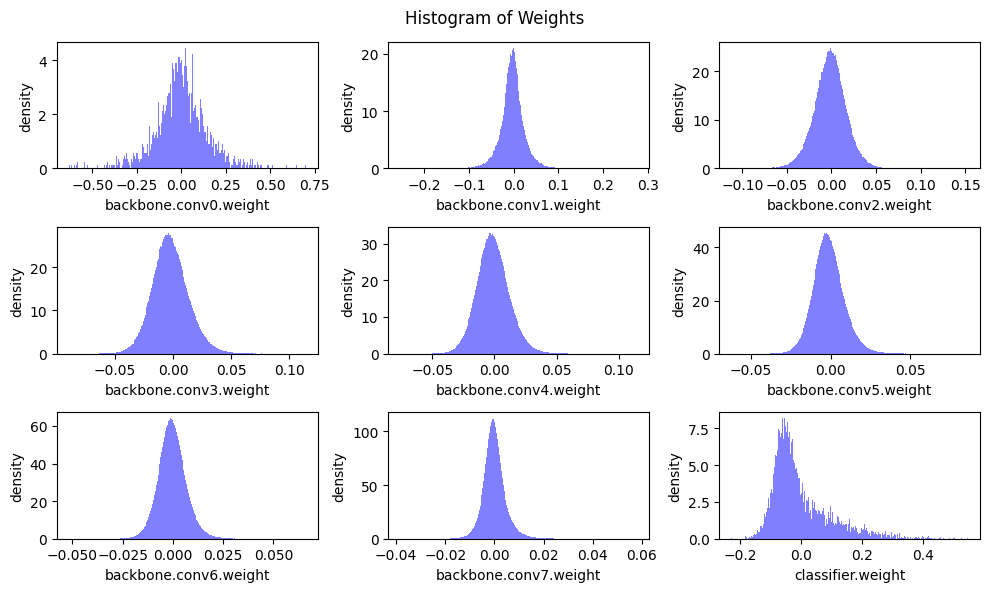
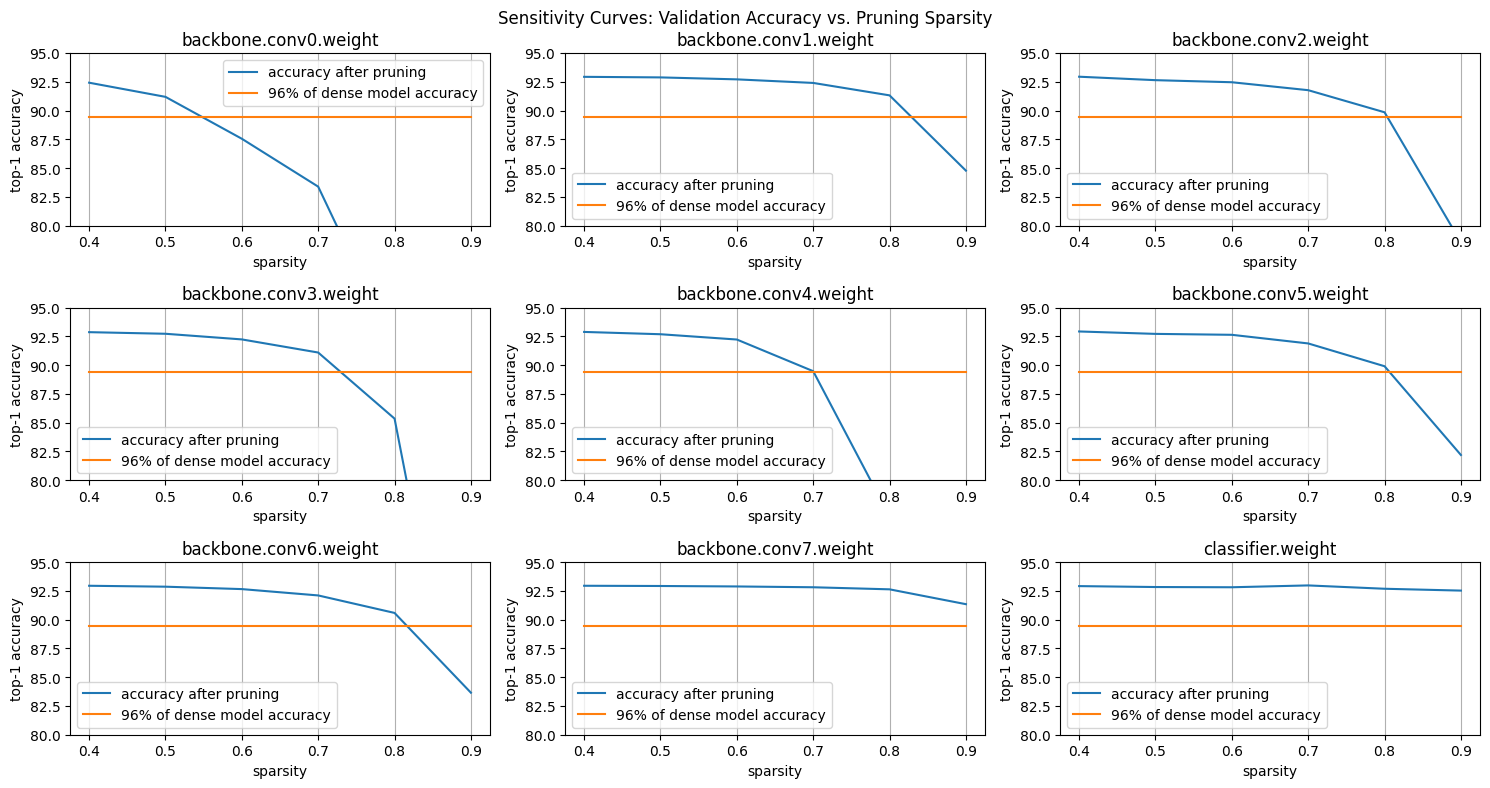
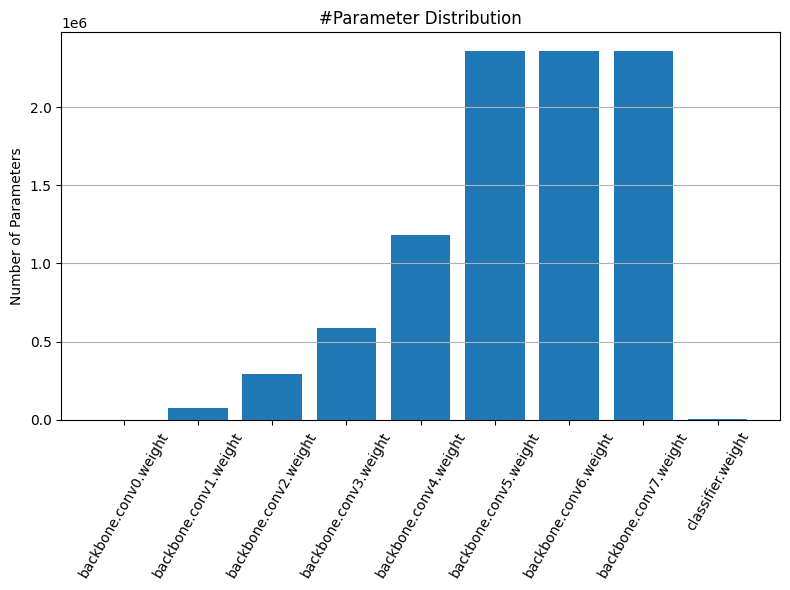
    sparsity=[0.40,0.50,0.60,0.70,0.80,0.90]: accuracy=[92.42%, 91.19%, 87.55%, 83.39%, 69.41%, 31.81%]    sparsity=[0.40,0.50,0.60,0.70,0.80,0.90]: accuracy=[92.93%, 92.88%, 92.71%, 92.40%, 91.32%, 84.78%]    sparsity=[0.40,0.50,0.60,0.70,0.80,0.90]: accuracy=[92.94%, 92.64%, 92.46%, 91.77%, 89.85%, 78.56%]    sparsity=[0.40,0.50,0.60,0.70,0.80,0.90]: accuracy=[92.86%, 92.72%, 92.23%, 91.09%, 85.35%, 51.31%]    sparsity=[0.40,0.50,0.60,0.70,0.80,0.90]: accuracy=[92.88%, 92.68%, 92.22%, 89.47%, 76.86%, 38.78%]    sparsity=[0.40,0.50,0.60,0.70,0.80,0.90]: accuracy=[92.92%, 92.71%, 92.63%, 91.88%, 89.90%, 82.19%]    sparsity=[0.40,0.50,0.60,0.70,0.80,0.90]: accuracy=[92.94%, 92.86%, 92.65%, 92.10%, 90.58%, 83.65%]    sparsity=[0.40,0.50,0.60,0.70,0.80,0.90]: accuracy=[92.94%, 92.92%, 92.88%, 92.81%, 92.63%, 91.34%]    sparsity=[0.40,0.50,0.60,0.70,0.80,0.90]: accuracy=[92.91%, 92.83%, 92.81%, 92.97%, 92.68%, 92.52%]

def plot_sensitivity_scan(sparsities, accuracies, dense_model_accuracy):
    lower_bound_accuracy = 100 - (100 - dense_model_accuracy) * 1.5
    fig, axes = plt.subplots(3, int(math.ceil(len(accuracies) / 3)),figsize=(15,8))
    axes = axes.ravel()
    plot_index = 0
    for name, param in model.named_parameters():
        if param.dim() > 1:
            ax = axes[plot_index]
            curve = ax.plot(sparsities, accuracies[plot_index])
            line = ax.plot(sparsities, [lower_bound_accuracy] * len(sparsities))
            ax.set_xticks(np.arange(start=0.4, stop=1.0, step=0.1))
            ax.set_ylim(80, 95)
            ax.set_title(name)
            ax.set_xlabel('sparsity')
            ax.set_ylabel('top-1 accuracy')
            ax.legend([
                'accuracy after pruning',
                f'{lower_bound_accuracy / dense_model_accuracy * 100:.0f}% of dense model accuracy'
            ])
            ax.grid(axis='x')
            plot_index += 1
    fig.suptitle('Sensitivity Curves: Validation Accuracy vs. Pruning Sparsity')
    fig.tight_layout()
    fig.subplots_adjust(top=0.925)
    plt.show()

plot_sensitivity_scan(sparsities, accuracies, dense_model_accuracy)

Question 4 (15 pts)

위 sensitivity curves의 정보를 사용하여 다음 질문에 답해 주세요.

Question 4.1 (5 pts)

pruning sparsity와 모델 정확도 사이의 관계는 무엇인가요? (즉, sparsity가 높아질 때 정확도가 증가하나요, 아니면 감소하나요?)

Your Answer:

pruning sparsity가 높아질 수록, model accuracy는 감소하는 경향을 보인다

Question 4.2 (5 pts)

모든 레이어가 같은 sensitivity를 가지고 있나요?

Your Answer:

어떤 레이어는 sensitive하지 않고(classifier), 어떤 레이어는 sensitive하다(conv0) 대체로, 앞쪽 레이어(0~1..)이 민감해보인다

Question 4.3 (5 pts)

어떤 레이어가 pruning sparsity에 가장 민감한가요?

Your Answer:

conv0 layer

#Parameters of each layer

정확도뿐만 아니라 각 레이어의 매개변수(parameter) 수도 sparsity 선택에 영향을 미칩니다. 매개변수가 더 많은 레이어는 더 큰 sparsities를 요구합니다.

다음 코드 셀을 실행하여 전체 모델에서 #parameters의 분포를 그려주세요.

def plot_num_parameters_distribution(model):
    num_parameters = dict()
    for name, param in model.named_parameters():
        if param.dim() > 1:
            num_parameters[name] = param.numel()
    fig = plt.figure(figsize=(8, 6))
    plt.grid(axis='y')
    plt.bar(list(num_parameters.keys()), list(num_parameters.values()))
    plt.title('#Parameter Distribution')
    plt.ylabel('Number of Parameters')
    plt.xticks(rotation=60)
    plt.tight_layout()
    plt.show()

plot_num_parameters_distribution(model)

Sensitivity Curves와 #Parameters 분포를 기반으로 Sparsity 선택하기

Question 5 (10 pts)

sensitivity curves와 모델의 #parameters 분포를 기반으로 각 레이어의 sparsity를 선택해 주세요.

pruned 모델의 전체 압축 비율은 대체로 #parameters가 큰 레이어에 주로 의존하며, 다른 레이어는 pruning에 대한 sensitivity가 다릅니다(Question 4 참조).

pruning 후에 sparse 모델이 dense 모델의 크기의 25%이며, finetuning 후에 검증 정확도가 92.5% 이상인지 확인하세요.

Hint:

• #parameters가 더 많은 레이어는 더 큰 sparsity를 가져야 합니다. (Figure #Parameter Distribution 참조)
• pruning sparsity에 민감한 레이어(즉, sparsity가 높아질수록 정확도가 빠르게 떨어지는 레이어)는 더 작은 sparsity를 가져야 합니다. (Figure Sensitivity Curves 참조)

recover_model()

sparsity_dict = {
##################### YOUR CODE STARTS HERE #####################
    # please modify the sparsity value of each layer
    # please DO NOT modify the key of sparsity_dict
    'backbone.conv0.weight': 0,
    'backbone.conv1.weight': 0.5,
    'backbone.conv2.weight': 0.5,
    'backbone.conv3.weight': 0.5,
    'backbone.conv4.weight': 0.5,
    'backbone.conv5.weight': 0.8,
    'backbone.conv6.weight': 0.8,
    'backbone.conv7.weight': 0.9,
    'classifier.weight': 0
##################### YOUR CODE ENDS HERE #######################
}

정의된 sparsity_dict에 따라 모델을 prune하고 sparse 모델의 정보를 출력하기 위해 다음 셀을 실행해 주세요.

pruner = FineGrainedPruner(model, sparsity_dict)
print(f'After pruning with sparsity dictionary')
for name, sparsity in sparsity_dict.items():
    print(f'  {name}: {sparsity:.2f}')
print(f'The sparsity of each layer becomes')
for name, param in model.named_parameters():
    if name in sparsity_dict:
        print(f'  {name}: {get_sparsity(param):.2f}')

sparse_model_size = get_model_size(model, count_nonzero_only=True)
print(f"Sparse model has size={sparse_model_size / MiB:.2f} MiB = {sparse_model_size / dense_model_size * 100:.2f}% of dense model size")
sparse_model_accuracy = evaluate(model, dataloader['test'])
print(f"Sparse model has accuracy={sparse_model_accuracy:.2f}% before fintuning")

plot_weight_distribution(model, count_nonzero_only=True)

After pruning with sparsity dictionary
  backbone.conv0.weight: 0.00
  backbone.conv1.weight: 0.50
  backbone.conv2.weight: 0.50
  backbone.conv3.weight: 0.50
  backbone.conv4.weight: 0.50
  backbone.conv5.weight: 0.80
  backbone.conv6.weight: 0.80
  backbone.conv7.weight: 0.90
  classifier.weight: 0.00
The sparsity of each layer becomes
  backbone.conv0.weight: 0.00
  backbone.conv1.weight: 0.50
  backbone.conv2.weight: 0.50
  backbone.conv3.weight: 0.50
  backbone.conv4.weight: 0.50
  backbone.conv5.weight: 0.80
  backbone.conv6.weight: 0.80
  backbone.conv7.weight: 0.90
  classifier.weight: 0.00
Sparse model has size=8.63 MiB = 24.50% of dense model size
Sparse model has accuracy=87.00% before fintuning

Finetune the fine-grained pruned model

이전 셀의 출력에서 볼 수 있듯이, fine-grained pruning이 모델 가중치의 대부분을 줄이지만 모델의 정확도도 떨어졌습니다. 따라서, sparse 모델의 정확도를 회복하기 위해 finetune해야 합니다.

sparse 모델을 finetune하기 위해 다음 셀을 실행해 주세요. 완료하는 데 약 3분 정도 걸릴 것입니다.

num_finetune_epochs = 5
optimizer = torch.optim.SGD(model.parameters(), lr=0.01, momentum=0.9, weight_decay=1e-4)
scheduler = torch.optim.lr_scheduler.CosineAnnealingLR(optimizer, num_finetune_epochs)
criterion = nn.CrossEntropyLoss()

best_sparse_model_checkpoint = dict()
best_accuracy = 0
print(f'Finetuning Fine-grained Pruned Sparse Model')
for epoch in range(num_finetune_epochs):
    # At the end of each train iteration, we have to apply the pruning mask
    #    to keep the model sparse during the training
    train(model, dataloader['train'], criterion, optimizer, scheduler,
          callbacks=[lambda: pruner.apply(model)])
    accuracy = evaluate(model, dataloader['test'])
    is_best = accuracy > best_accuracy
    if is_best:
        best_sparse_model_checkpoint['state_dict'] = copy.deepcopy(model.state_dict())
        best_accuracy = accuracy
    print(f'    Epoch {epoch+1} Accuracy {accuracy:.2f}% / Best Accuracy: {best_accuracy:.2f}%')

Finetuning Fine-grained Pruned Sparse Model
    Epoch 1 Accuracy 92.66% / Best Accuracy: 92.66%
    Epoch 2 Accuracy 92.77% / Best Accuracy: 92.77%
    Epoch 3 Accuracy 92.80% / Best Accuracy: 92.80%
    Epoch 4 Accuracy 92.68% / Best Accuracy: 92.80%
    Epoch 5 Accuracy 92.77% / Best Accuracy: 92.80%

best finetuned sparse 모델의 정보를 보기 위해 다음 셀을 실행해 주세요.

# load the best sparse model checkpoint to evaluate the final performance
model.load_state_dict(best_sparse_model_checkpoint['state_dict'])
sparse_model_size = get_model_size(model, count_nonzero_only=True)
print(f"Sparse model has size={sparse_model_size / MiB:.2f} MiB = {sparse_model_size / dense_model_size * 100:.2f}% of dense model size")
sparse_model_accuracy = evaluate(model, dataloader['test'])
print(f"Sparse model has accuracy={sparse_model_accuracy:.2f}% after fintuning")

Sparse model has size=8.63 MiB = 24.50% of dense model size
Sparse model has accuracy=92.80% after fintuning

Channel Pruning

이 섹션에서는 channel pruning을 구현할 것입니다. Channel pruning은 전체 채널을 제거하여 기존 하드웨어(예: GPU)에서 추론 속도를 향상시킬 수 있습니다. 마찬가지로, 더 작은 크기(Frobenius norm으로 측정)의 가중치를 가진 채널을 제거합니다.

# firstly, let's restore the model weights to the original dense version
#   and check the validation accuracy
recover_model()
dense_model_accuracy = evaluate(model, dataloader['test'])
print(f"dense model has accuracy={dense_model_accuracy:.2f}%")

dense model has accuracy=92.95%

Remove Channel Weights

Fine-grained pruning과 달리, channel pruning에서는 텐서에서 가중치를 완전히 제거할 수 있습니다. 즉, 출력 채널의 수가 줄어듭니다:

\(\#\mathrm{out\_channels}_{\mathrm{new}} = \#\mathrm{out\_channels}_{\mathrm{origin}} \cdot (1 - \mathrm{sparsity})\)

Channel pruning 후에도 가중치 텐서 \(W\)는 여전히 dense합니다. 따라서, sparsity를 prune ratio라고 합니다.

Fine-grained pruning처럼, 다른 레이어에 대해 다른 pruning 비율을 사용할 수 있습니다. 하지만 지금은 모든 레이어에 대해 균일한 pruning 비율을 사용합니다. 우리는 대략 30%의 균일한 pruning 비율로 2배의 계산 감소를 목표로 합니다(왜 그런지 생각해 보세요).

이 섹션의 끝에서 레이어별로 다른 pruning 비율을 시도해 볼 수 있습니다. channel_prune 함수에 비율 리스트를 전달할 수 있습니다.

Question 6 (10 pts)

Channel pruning을 위한 다음 함수를 완성해 주세요.

여기서 우리는 첫 번째 \(\#\mathrm{out\_channels}_{\mathrm{new}}\) 채널을 제외한 모든 출력 채널을 단순히 prune합니다.

def get_num_channels_to_keep(channels: int, prune_ratio: float) -> int:
    """A function to calculate the number of layers to PRESERVE after pruning
    Note that preserve_rate = 1. - prune_ratio
    """
    ##################### YOUR CODE STARTS HERE #####################
    return int(round((1-prune_ratio)*channels))
    ##################### YOUR CODE ENDS HERE #####################

@torch.no_grad()
def channel_prune(model: nn.Module,
                  prune_ratio: Union[List, float]) -> nn.Module:
    """Apply channel pruning to each of the conv layer in the backbone
    Note that for prune_ratio, we can either provide a floating-point number,
    indicating that we use a uniform pruning rate for all layers, or a list of
    numbers to indicate per-layer pruning rate.
    """
    # sanity check of provided prune_ratio
    assert isinstance(prune_ratio, (float, list))
    n_conv = len([m for m in model.backbone if isinstance(m, nn.Conv2d)])
    # note that for the ratios, it affects the previous conv output and next
    # conv input, i.e., conv0 - ratio0 - conv1 - ratio1-...
    if isinstance(prune_ratio, list):
        assert len(prune_ratio) == n_conv - 1
    else:  # convert float to list
        prune_ratio = [prune_ratio] * (n_conv - 1)

    # we prune the convs in the backbone with a uniform ratio
    model = copy.deepcopy(model)  # prevent overwrite
    # we only apply pruning to the backbone features
    all_convs = [m for m in model.backbone if isinstance(m, nn.Conv2d)]
    all_bns = [m for m in model.backbone if isinstance(m, nn.BatchNorm2d)]
    # apply pruning. we naively keep the first k channels
    assert len(all_convs) == len(all_bns)
    for i_ratio, p_ratio in enumerate(prune_ratio):
        prev_conv = all_convs[i_ratio]
        prev_bn = all_bns[i_ratio]
        next_conv = all_convs[i_ratio + 1]
        original_channels = prev_conv.out_channels  # same as next_conv.in_channels
        n_keep = get_num_channels_to_keep(original_channels, p_ratio)

        # prune the output of the previous conv and bn
        prev_conv.weight.set_(prev_conv.weight.detach()[:n_keep])
        prev_bn.weight.set_(prev_bn.weight.detach()[:n_keep])
        prev_bn.bias.set_(prev_bn.bias.detach()[:n_keep])
        prev_bn.running_mean.set_(prev_bn.running_mean.detach()[:n_keep])
        prev_bn.running_var.set_(prev_bn.running_var.detach()[:n_keep])

        # prune the input of the next conv (hint: just one line of code)
        ##################### YOUR CODE STARTS HERE #####################
        next_conv.weight.set_(next_conv.weight.detach()[:, :n_keep])
        ##################### YOUR CODE ENDS HERE #####################

    return model

구현이 올바른지 확인하기 위해 다음 셀을 실행하여 확인하세요.

dummy_input = torch.randn(1, 3, 32, 32).cuda()
pruned_model = channel_prune(model, prune_ratio=0.3)
pruned_macs = get_model_macs(pruned_model, dummy_input)
assert pruned_macs == 305388064
print('* Check passed. Right MACs for the pruned model.')

* Check passed. Right MACs for the pruned model.

이제 30% pruning 비율을 가진 균일 channel pruning 후 모델의 성능을 평가해 봅시다.

직접적으로 30%의 채널을 제거하는 것은 낮은 정확도로 이어집니다.

pruned_model_accuracy = evaluate(pruned_model, dataloader['test'])
print(f"pruned model has accuracy={pruned_model_accuracy:.2f}%")

pruned model has accuracy=28.14%

Ranking Channels by Importance

보시다시피, 모든 레이어에서 첫 30%의 채널을 제거하면 정확도가 크게 감소합니다. 이 문제를 해결하는 한 가지 가능한 방법은 덜 중요한 채널 가중치를 찾아서 제거하는 것입니다. 중요도를 평가하는 인기 있는 기준은 각 입력 채널에 해당하는 가중치의 Frobenius norm을 사용하는 것입니다:

\(importance_{i} = \|W_{i}\|_2, \;\; i = 0, 1, 2,\cdots, \#\mathrm{in\_channels}-1\)

우리는 채널 가중치를 더 중요한 것에서 덜 중요한 것으로 정렬한 다음, 각 레이어에 대해 처음 \(k\)개의 채널을 유지할 수 있습니다.

Question 7 (15 pts)

Frobenius norm에 기반하여 가중치 텐서를 정렬하는 다음 함수를 완성해 주세요.

Hint:

• 텐서의 Frobenius norm을 계산하기 위해, Pytorch는 torch.norm API를 제공합니다.

# function to sort the channels from important to non-important
def get_input_channel_importance(weight):
    in_channels = weight.shape[1]
    importances = []
    # compute the importance for each input channel
    for i_c in range(weight.shape[1]):
        channel_weight = weight.detach()[:, i_c]
        ##################### YOUR CODE STARTS HERE #####################
        importance = torch.norm(channel_weight, p=2)
        ##################### YOUR CODE ENDS HERE #####################
        importances.append(importance.view(1))
    return torch.cat(importances)

@torch.no_grad()
def apply_channel_sorting(model):
    model = copy.deepcopy(model)  # do not modify the original model
    # fetch all the conv and bn layers from the backbone
    all_convs = [m for m in model.backbone if isinstance(m, nn.Conv2d)]
    all_bns = [m for m in model.backbone if isinstance(m, nn.BatchNorm2d)]
    # iterate through conv layers
    for i_conv in range(len(all_convs) - 1):
        # each channel sorting index, we need to apply it to:
        # - the output dimension of the previous conv
        # - the previous BN layer
        # - the input dimension of the next conv (we compute importance here)
        prev_conv = all_convs[i_conv]
        prev_bn = all_bns[i_conv]
        next_conv = all_convs[i_conv + 1]
        # note that we always compute the importance according to input channels
        importance = get_input_channel_importance(next_conv.weight)
        # sorting from large to small
        sort_idx = torch.argsort(importance, descending=True)

        # apply to previous conv and its following bn
        prev_conv.weight.copy_(torch.index_select(
            prev_conv.weight.detach(), 0, sort_idx))
        for tensor_name in ['weight', 'bias', 'running_mean', 'running_var']:
            tensor_to_apply = getattr(prev_bn, tensor_name)
            tensor_to_apply.copy_(
                torch.index_select(tensor_to_apply.detach(), 0, sort_idx)
            )

        # apply to the next conv input (hint: one line of code)
        ##################### YOUR CODE STARTS HERE #####################
        next_conv.weight.copy_(torch.index_select(next_conv.weight.detach(), 1, sort_idx))
        ##################### YOUR CODE ENDS HERE #####################

    return model

이제 다음 셀을 실행하여 결과가 올바른지 확인하세요.

print('Before sorting...')
dense_model_accuracy = evaluate(model, dataloader['test'])
print(f"dense model has accuracy={dense_model_accuracy:.2f}%")

print('After sorting...')
sorted_model = apply_channel_sorting(model)
sorted_model_accuracy = evaluate(sorted_model, dataloader['test'])
print(f"sorted model has accuracy={sorted_model_accuracy:.2f}%")

# make sure accuracy does not change after sorting, since it is
# equivalent transform
assert abs(sorted_model_accuracy - dense_model_accuracy) < 0.1
print('* Check passed.')

Before sorting...
dense model has accuracy=92.95%
After sorting...
sorted model has accuracy=92.95%
* Check passed.

마지막으로 프루닝된 모델의 정확도를 정렬할 때와 그렇지 않을 때를 비교합니다.

channel_pruning_ratio = 0.3  # pruned-out ratio

print(" * Without sorting...")
pruned_model = channel_prune(model, channel_pruning_ratio)
pruned_model_accuracy = evaluate(pruned_model, dataloader['test'])
print(f"pruned model has accuracy={pruned_model_accuracy:.2f}%")


print(" * With sorting...")
sorted_model = apply_channel_sorting(model)
pruned_model = channel_prune(sorted_model, channel_pruning_ratio)
pruned_model_accuracy = evaluate(pruned_model, dataloader['test'])
print(f"pruned model has accuracy={pruned_model_accuracy:.2f}%")

 * Without sorting...
pruned model has accuracy=28.14%
 * With sorting...
pruned model has accuracy=36.81%

보시다시피 channel sorting은 pruned model의 정확도를 약간 향상시킬 수 있지만 여전히 channel pruning에 매우 일반적인 큰 저하가 있는 걸 알 수 있습니다. 이러한 정확도 저하를 회복하기 위해 fine-tuning을 수행할 수 있습니다.

num_finetune_epochs = 5
optimizer = torch.optim.SGD(pruned_model.parameters(), lr=0.01, momentum=0.9, weight_decay=1e-4)
scheduler = torch.optim.lr_scheduler.CosineAnnealingLR(optimizer, num_finetune_epochs)
criterion = nn.CrossEntropyLoss()

best_accuracy = 0
for epoch in range(num_finetune_epochs):
    train(pruned_model, dataloader['train'], criterion, optimizer, scheduler)
    accuracy = evaluate(pruned_model, dataloader['test'])
    is_best = accuracy > best_accuracy
    if is_best:
        best_accuracy = accuracy
    print(f'Epoch {epoch+1} Accuracy {accuracy:.2f}% / Best Accuracy: {best_accuracy:.2f}%')

Epoch 1 Accuracy 91.66% / Best Accuracy: 91.66%
Epoch 2 Accuracy 92.10% / Best Accuracy: 92.10%
Epoch 3 Accuracy 92.01% / Best Accuracy: 92.10%
Epoch 4 Accuracy 92.18% / Best Accuracy: 92.18%
Epoch 5 Accuracy 92.16% / Best Accuracy: 92.18%

Measure acceleration from pruning

fine-tuning이 끝나면 모델은 정확도를 거의 회복합니다. channel pruning는 fine-grained pruning에 비해 일반적으로 정확도를 회복하기가 더 어렵다는 것을 이미 알고 계실 수도 있습니다. 그러나 specialized model format이 없으면 직접적으로 모델 크기가 작아지고 계산이 작아집니다. GPU에서도 더 빠르게 실행될 수 있습니다.

이제 pruned model의 모델 크기, 계산 및 지연 시간을 비교해봅시다.

# helper functions to measure latency of a regular PyTorch models.
#   Unlike fine-grained pruning, channel pruning
#   can directly leads to model size reduction and speed up.
@torch.no_grad()
def measure_latency(model, dummy_input, n_warmup=20, n_test=100):
    model.eval()
    # warmup
    for _ in range(n_warmup):
        _ = model(dummy_input)
    # real test
    t1 = time.time()
    for _ in range(n_test):
        _ = model(dummy_input)
    t2 = time.time()
    return (t2 - t1) / n_test  # average latency

table_template = "{:<15} {:<15} {:<15} {:<15}"
print (table_template.format('', 'Original','Pruned','Reduction Ratio'))

# 1. measure the latency of the original model and the pruned model on CPU
#   which simulates inference on an edge device
dummy_input = torch.randn(1, 3, 32, 32).to('cpu')
pruned_model = pruned_model.to('cpu')
model = model.to('cpu')

pruned_latency = measure_latency(pruned_model, dummy_input)
original_latency = measure_latency(model, dummy_input)
print(table_template.format('Latency (ms)',
                            round(original_latency * 1000, 1),
                            round(pruned_latency * 1000, 1),
                            round(original_latency / pruned_latency, 1)))

# 2. measure the computation (MACs)
original_macs = get_model_macs(model, dummy_input)
pruned_macs = get_model_macs(pruned_model, dummy_input)
print(table_template.format('MACs (M)',
                            round(original_macs / 1e6),
                            round(pruned_macs / 1e6),
                            round(original_macs / pruned_macs, 1)))

# 3. measure the model size (params)
original_param = get_num_parameters(model)
pruned_param = get_num_parameters(pruned_model)
print(table_template.format('Param (M)',
                            round(original_param / 1e6, 2),
                            round(pruned_param / 1e6, 2),
                            round(original_param / pruned_param, 1)))

# put model back to cuda
pruned_model = pruned_model.to('cuda')
model = model.to('cuda')

                Original        Pruned          Reduction Ratio
Latency (ms)    24.2            13.0            1.9            
MACs (M)        606             305             2.0            
Param (M)       9.23            5.01            1.8            

Question 8 (10 pts)

이전 코드셀의 정보를 이용하여 다음 질문에 답변해 주시기 바랍니다.

Question 8.1 (5 pts)

30%의 채널을 제거하면 대략 50%의 계산 절감 효과가 발생하는 이유를 설명하세요.

Your Answer:

MAC은 2배, Param은 1.8배 줄어들었지만, latency는 1.7배만 더 빨라졌다 메모리 관련된 이유라고 추정됨

Question 8.2 (5 pts)

지연 시간 감소 비율(latency reduction ratio)이 계산 감소(computation reduction)보다 약간 작은 이유를 설명하세요.

Your Answer:

0.7^2 = 0.49 니까, 얼추 2배. 파라미터 수가 줄어들수록 latency는 quadratic하게 줄어든다

---

Compare Fine-grained Pruning and Channel Pruning

Question 9 (10 pts)

이번 랩에서 모든 실험을 한 후에는 fine-grained pruning와 channel pruning에 익숙해질 수 있습니다.

lecture와 이번 lab에서 배운 내용을 활용하여 다음 질문에 답변해 주시기 바랍니다.

Question 9.1 (5 pts)

fine-grained pruning와 channel pruning의 장단점은 무엇입니까?

compression ratio, accuracy, latency, hardware support(i.e., 전문 하드웨어 가속기 필요) 등의 관점에서 논의할 수 있습니다.

Your Answer:

1. fine-grained

• 장점
  • 정확도가 높음
  • Usually larger compression ratio since we can flexibly find “redundant” weights
• 단점
  • cpu overhead
  • memory overhead
  • hardware support 필요(eie…)

2. channel pruning

• 장점
  • 빠른 inference
• 단점
  • smaller compression ratio

Question 9.2 (5 pts)

스마트폰에서 모델을 더 빨리 실행시키고 싶다면, 어떤 가지치기 방법을 사용할 것인가요? 그 이유는 무엇인가요?

Your Answer:

특별한 하드웨어 서포트가 필요하지않고, inference time이 빠른 channel pruning.